Do you enjoy solving puzzles and brain teasers? If so, you may be familiar with the concept of computational complexity. It’s an intriguing field of computer science and mathematics that studies how efficiently a problem can be solved using algorithms and computers.

For me, one of the most fascinating problems in computational complexity theory is the P vs. NP enigma. Why is it so crucial? And what does it have to do with popular games like Tetris, Sudoku, and Super Mario? Let me break it down for you.   

The spectrum of problem-solving

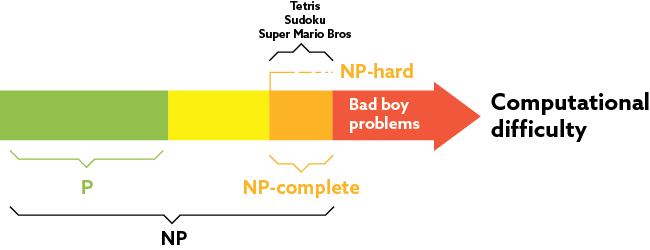
Since the dawn of time, people have been solving problems. But not every problem is as difficult as the next. In fact, some problems are much easier to solve with computers than others. We can visualize that by looking at computational difficulty as something that increases as you move along a line like this:

P: predictable problems

On this line, something on the left is easier than something on the right. Sorting a list of names alphabetically is — unsurprisingly — an easy problem to solve. But sorting is boring, simply because it’s so easy. These easy (boring) problems are all in a set we will call P. The easiest problems we know are problems in the P set.

NP: challenging, but solvable problems 

There are other — more interesting (read: more difficult) — problems like Tetris, or (generalized) Sudoku, or even Super Mario Bros. Let’s put these difficult problems in another set, namely NP. What’s so special about the problems in NP? Well, if you propose a solution to a problem in NP, a computer can easily check whether it is valid.

For example, in Tetris: if I’m given a series of blocks to position in a particular way in a given situation, then a computer can easily check whether I’ll ‘survive’ (assuming my fingers are quick enough to get the blocks right, but for a computer that’s clearly not a problem). Or in Sudoku, if I put a particular number in a particular square, the computer can easily check whether the proposed solution is sure to be correct (meaning that there can be no other number in that same square). And in Super Mario Bros, I can easily carry out the list of suggested moves to see if it gets Mario from A to B.

Of course, that means that every problem in P is also in NP. Let’s update our line with the new set NP:

What’s the fundamental difference between P and NP problems? The answer is complexity. It’s much more difficult to quickly find a solution to an NP problem than a P problem. Computers can easily check solutions to NP problems, but devising an algorithm that can propose solutions to NP problems in a reasonable time is much more difficult. That’s what makes NP more interesting!

NP-hard: bad boy problems

It turns out that there are some problems we don’t even know how to solve quickly with our current knowledge. We call this set of problems NP-hard, defined as all problems that are at least as hard as the hardest NP problem. This means that some of them are in NP, but some of them are outside NP. Here’s our updated line:

Some of these NP-hard problems are so tricky it’s not just difficult to find solutions, but it’s difficult even to check them! These are what I like to call the ‘bad boy’ problems, a subset of NP-hard.

NP-complete: the key to solving NP-problems

And let’s now also introduce the NP-complete subset for those NP-hard problems where solutions can be checked easily.

NP-complete problems are therefore problems that are in both NP and NP-hard. They’re really on the border between NP and the bad boys. And here’s a fundamental characteristic: if you can solve an NP-complete problem quickly, that means you can solve all the hardest problems in NP quickly and, therefore, you can solve them all quickly. So, solving an NP-complete problem quickly is like finding a master key. So, now the complete line looks like this.

Oh, and how about Tetris and the other examples I gave? Well, Tetris is not a bad boy problem but an NP-complete problem, meaning that solutions can be checked easily but we don’t know yet how to solve the problem quickly. Similarly, Sudoku and Super Mario Bros are also NP-complete problems. So, let’s add these to our line:

The enigma of P vs. NP: Is there a shortcut to solving hard problems?